16

поява машин

Станція метро Ар-е-Метьє (фр. Arts et M 'E tiers - «Мистецтва і ремесла») - одна з найбільш дивних в Парижі. Туристу, який опинився тут, може здатися, що він потрапив в мідний чрев гігантської підводного човна. Великі червонуваті заклепки йдуть від стелі по стінах, де також розташований десяток ілюмінаторів. Подивившись по сторонах, можна побачити цікаві сцени, що представляють різні стародавні винаходи, виглядають незвично. Еліптичні передачі, сферична астролябія, водяне колесо сусідять з космічним кораблем і сталевим конвертором. І якби не нескінченний потік вічно поспішають кудись підземними коридорами парижан, навряд чи хтось здивувався б, побачивши тут величну фігуру капітана Немо, що зійшов прямо зі сторінок роману Жюля Верна.

Оздоблення вестибюля метро - це лише початок того, що нас чекає на поверхні. Сьогодні я тримаю свій шлях в Консерваторію мистецтв і ремесел (фр. Conservatoire national des arts et m'etiers, CNAM), музей, в якому представлені найважливіші винаходи людства. Перші механізовані машини, телеграф, стрілочний індикатор, поршневий манометр, голландські автоматичні годинник, вольтів стовп, ткацький верстат, перфокарти, друкарський верстат, сифонні барометри - всі ці винаходи з минулого втягують мене в запаморочливий вихор технологічних відкриттів останніх чотирьох століть. Зупинившись в середині парадних сходів, я бачу аероплан XIX в. з гігантськими крилами, як у кажана. У кутку коридору стоїть перший марсохід Лама, розроблений російськими вченими в XX в.

Я швидко проходжу повз всіх цих неймовірних предметів і піднімаюся прямо на другий поверх. Тут розташована галерея лабораторних інструментів, серед яких можна знайти астрономічний телескоп, водяний годинник, компаси, ваги Роберваля, гігантські термометри і астрономічні глобуси, що підносяться на своїх осях! І раптом помічаю в кутку вітрини то, навіщо я сюди прийшов: лічильна машина Паскаля, або паскалина. Ця цікава річ являє собою латунну коробку 40 см в довжину і 20 см в ширину, на зовнішній стороні якої зображено шість пронумерованих рядів. Цей механізм розробив в 1642 р Блез Паскаль у віці всього 19 років. Переді мною знаходиться перша лічильна машина в історії.

Перша? Щоб бути до кінця відвертим, необхідно відзначити, що і до XVII ст. вже були можливості робити розрахунки. Так чи інакше, пальці виконували роль першого калькулятора всіх часів, а також представники Homo sapiens використовували різні аксесуари для ведення розрахунків. Кістки Ішанго з насічками на них, глиняні жетони з Урука, палички в Стародавньому Китаї або рахунки, які були дуже популярні в епоху Античності, - всі ці інструменти використовувалися для підрахунків і обчислень. Проте жоден з цих прикладів не підходить під визначення, яке, як правило, дається обчислювальним машинам.

Щоб розібратися, розглянемо детально механізм роботи рахунків. Цей математичний інструмент складається з безлічі спиць, за якими ковзають кісточки. Перший стрижень відповідає кількості одиниць, другий - десятків, третій - сотень і так далі. Так що якщо ви хочете вказати число 23, пересуньте дві кісточки в розряді десятків і три - в розряді одиниць. І якщо ви хочете додати до цього числа 45 - пересуньте чотири кісточки в розряді десятків і п'ять - в розряді одиниць, що, таким чином, дасть в сумі 68.

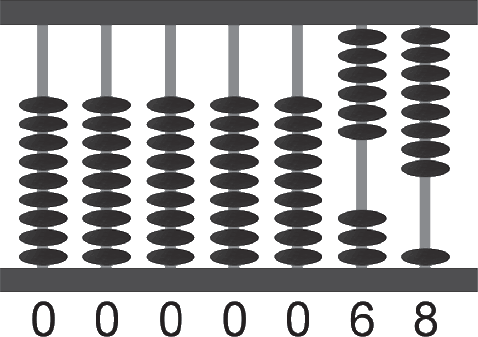
Якщо при додаванні цифр в одному розряді сума стає двозначною, необхідно зробити невелику додаткову маніпуляцію. Для того щоб додати 5 до 68 на спиці розряду одиниць, залишилася всього одна кісточка. Якщо на спиці не вистачає кісточок для виконання дії, то на ній залишають стільки кісточок, скільки не вистачило, а решта перекидають в іншу сторону, і додають ще одну кісточку в значення десятків. Таким чином, в сумі вийде 73.

Це зовсім не складна маніпуляція, але тільки з появою лічильної машини Паскаля і калькулятора почалася епоха обчислювальних машин. Для того щоб виконати ту ж саму операцію, користуючись обчислювальною машиною, уже не потрібно було тримати в умі числа. Такі апарати, по суті, не виконують обчислення самостійно, а просто допомагають людині фіксувати певні значення чисел. Користуючись же сучасним калькулятором, ви взагалі не будете замислюватися про те, як виконуються дії. Чи є в діях перенесення цифр в сусідній розряд - для вас вже не має значення! Більше немає необхідності тримати числа в розумі у відповідних ситуаціях, все зробить за вас машина.

Відповідна цим критерієм паскалина - дійсно перша лічильна машина в історії. Хоча механізм роботи вельми специфічний і вимагає великої майстерності для її виготовлення, принцип роботи лічильної машини Паскаля досить простий. На верхній частині машини розташовані шість коліщаток, на які нанесені поділки від 0 до 9.

Перше коліщатко справа позначає число одиниць, друге - десятків і так далі. Над коліщатками розташовані шість маленьких осередків, по одному для кожного коліщатка, в яких відображаються цифри. Для того щоб ввести число 28, необхідно просто повернути коліщатко десятків на два ділення за годинниковою стрілкою і коліщатко одиниць - на вісім поділів. За допомогою внутрішньої системи шестерень, в області відображення в сусідніх взаємопов'язаних осередках відобразяться 2 і 8. І тепер, якщо ви захочете додати 5 до цього числа, немає необхідності нічого тримати в умі: досить просто повернути коліщатко одиниць на п'ять поділок і, коли значення зміниться з 9 на 0, значення десятків автоматично зміниться з 2 на 3. значення, що відображається на машині, тепер так само 33.

І це працює в кожному з розрядів. Якщо набрати на паскалина 99 999 і повернути коліщатко одиниць на один оборот, то на апараті відобразиться 100 000, без необхідності в додаткових діях!

Після Паскаля багато винахідників намагалися удосконалити його винахід, щоб з його використанням можна було зробити швидко і ефективно більше дій. В кінці XVII ст. Лейбніц був одним з перших, хто розробив механізм для здійснення операцій множення і ділення. Його система була недосконалою і видавала неправильні рішення в деяких окремих випадках. Тільки в XVIII в. його ідеї втілилися в повному обсязі. Завдяки умінням і уяві винахідників були розроблені кілька більш надійних і ефективних прототипів. Однак через складність механізмів такі машини виявилися вельми великими, майже з комод розміром.

У XIX ст. рахункові машини стали більш доступні і поширені приблизно так само широко, як і інші, схожі на них апарати - друкарські машинки. Багато бухгалтерські фірми, підприємці і звичайні торговці починають користуватися калькуляторами, які швидко стали невід'ємною частиною інтер'єру і були незамінні в роботі. Стає складно уявити собі, як люди до сих пір обходилися без них.

Продовжуючи ходити по музею, я бачу ряд машин, сучасних паскалина. Тут представлені арифмометр Тома де Кольмара, машина множення Леона Болле, поліхромної арифмограф Дюбуа і комптометр Фелта і Таррант. Одним з найбільш популярних апаратів, які користувалися великим успіхом, був арифмометр, який розробив в Росії шведський інженер Вильгодт Теофіл Однер. Ця машина складається з трьох основних елементів: верхня частина, на якій за допомогою невеликих важелів виставляються необхідні числа, нижня частина, що складається з каретки, здатна зміщуватися в горизонтальному напрямку і на якій відображається результат операції, а праворуч розташована рукоятка, при обертанні якої виробляються арифметичні дії .

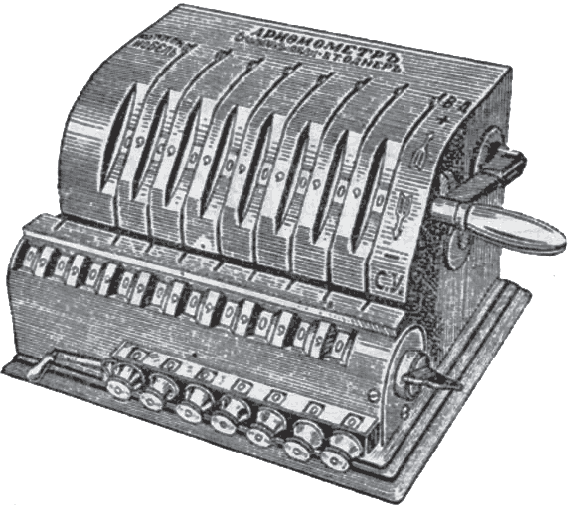
При кожному повороті рукоятки число в верхній частині додається до числа, вже отображаемому на нижній каретці. Для того щоб зробити віднімання, досить повернути рукоятку в іншу сторону.

Тепер уявіть, що вам необхідно виконати множення 374 x 523. Вкажіть число 374 у верхній частині і поверніть рукоятку три рази. У нижній частині відобразиться 1 122, результат операції 374 x 3. Наведіть тепер каретку на розряд десятків і поверніть рукоятку ще два рази. Вийде 8602, що відповідає добутку 374 і 23. Наведіть каретку ще на один розряд - до сотень - і поверніть рукоятку на п'ять обертів, і ви отримаєте результат: 195 602. Трохи потренувавшись, ви зможете виробляти множення за кілька секунд.

У 1834 р на розум англійського математика Чарльза Баббедж приходить щонайменше безглузда ідея поєднати лічильну машину з ткацьким верстатом! У ті роки робота ткацького верстата зазнала ряд удосконалень. Одним з них стало впровадження перфокарт, що забезпечило використання одного верстата для виготовлення тканин з різними візерунками, не змінюючи його параметри. Залежно від наявності або відсутності отвори в карті, шарнірний гак проходить або не проходить, а уточнюючи нитка проходить вище або нижче основної тканини. Таким чином, досить перенести бажаний малюнок на перфокарту і помістити її в машину.

Виходячи з властивостей цієї моделі, Чарлз Беббідж задумав створити механічний калькулятор, здатний не тільки здійснювати такі дії, як, наприклад, додавання множення, а й адаптуватися і виконувати мільйони різних операцій в залежності від того, яка перфокарта буде в нього вставлена. Якщо бути більш точним, ця машина може виконувати будь-які поліноміальні дії, тобто розрахунки, що поєднують в довільному порядку чотири основні операції та піднесення до степеня. Аналогічним чином тому, як на паскалина потрібно було виконувати одні і ті ж маніпуляції, незалежно від вихідних чисел, машина Беббіджа дозволяла виробляти одні й ті ж маніпуляції, незалежно від виконуваних дій. Більше не було необхідності, як у випадку, наприклад, з арифмометром Однера, обертати рукоятку в протилежному напрямку в залежності від того, що потрібно виконати - додавання чи віднімання. Досить просто записати необхідні дії на перфокарте, і машина сама про все подбає. Завдяки цій революційної функції винахід Беббіджа прийнято вважати першою в історії обчислювальної машиною.

Використання такої машини кидало новий виклик. Щоб виконати розрахунок з її допомогою, необхідно було забезпечити можливість виготовлення відповідних перфокарт, що складаються з послідовності отворів і суцільних місць, які вловлює механізм, внаслідок чого будуть виконуватися всі операції дію за дією. Таким чином, усі користувачі повинен перед початком її використання створити відповідну перфокарту.

Розробкою пристрою, здатного переводити необхідні обчислення на мову математики, займалася британський математик Ада Лавлейс, яка вела дослідження в даній області. Вона досліджувала функціонал машини і прийшла до висновку, що сам Беббідж не уявляв її потенціал. Лавлейс створить складний код для обчислення послідовності Бернуллі, що було надзвичайно корисним в обчисленні нескінченно малих величин послідовності, виявленої за більш ніж сто років до того швейцарським математиком Якобом Бернуллі. Цей код прийнято вважати першою комп'ютерною програмою, що робить, таким чином, Лавлейс першим програмістом в історії.

Ада Лавлейс померла в 1852 р у віці 36 років. Чарльз Беббідж протягом усього життя намагався побудувати свою машину, але помер в 1871 р, так і не дочекавшись завершення виготовлення її прототипу. Тільки в XX в. вдалося нарешті побачити роботу машини Беббіджа в дії. Спостерігати за одним з таких калькуляторів - це воістину приголомшливе і чарівне видовище. Його значний розмір (висотою приблизно в два метри і шириною в три) і робота сотень шестерень, які рухаються всередині, одночасно вражає і дивує.

Незавершений прототип апарату, розробкою якого займався британський вчений, в даний час зберігається в Музеї науки в Лондоні. Функціонуючу копію, відтворену на початку XXI ст., Можна побачити в Музеї комп'ютерної історії в Маунтін-В'ю, штат Каліфорнія.

У XX ст. використання обчислювальних машин досягне такого рівня, про який Беббідж і Лавлейс навіть не могли подумати. Калькулятори знайдуть своє застосування для вирішення як найдавніших, так і зовсім нових математичних задач.

З одного боку, обчислення нескінченно малих величин і уявні числа дозволили описати у вигляді рівнянь електромагнітні явища, які незабаром будуть застосовані в електронних пристроях. З іншого боку, в XIX в. були заново підняті питання, що зачіпали фундаментальні основи математики, аксіоми і міркування в доказах. Так, з одного боку, у машин з'явилася високоефективна інфраструктура, а з іншого - можливість здійснювати найпростіші дії для знаходження рішення більш складних завдань.

Одним з головних діячів цієї революції був британський математик Алан Тьюринг. У 1936 р він опублікував статтю, в якій провів паралель між можливістю довести теорему за допомогою математики і здатністю знайти рішення за допомогою обчислювальних машин з використанням досягнень інформатики. Він вперше описує принцип дії машини, згодом названої в його честь, який до цих пір широко використовується в теоретичних засадах обчислювальної техніки. Машина Тьюринга була теоретичною конструкцією. Британський математик не займався розробкою конкретних механізмів, за допомогою яких така машина могла б працювати. Він всього лише оцінював основні операції, які могли б виконуватися на його машині, і задавався питанням, який результат можна отримати, комбінуючи їх. Тут простежується чітка аналогія з тим, як в математиці, виходячи з сформульованих аксіом, вчені потім намагаються вивести теореми, грунтуючись на них.

Набір інструкцій, які задаються машині для досягнення результату, називається алгоритмом. Цей термін походить від латинського варіанту написання імені аль-Хорезмі. Необхідно відзначити, що обчислювальні алгоритми будуть в значній мірі спиратися на вирішення завдань, відомі вже з давніх пір. Пам'ятайте, як аль-Хорезмі у своїй книзі «Кітаб аль-джебр ва-ль-мукабала» не тільки розглядав абстрактні математичні об'єкти, але і давав практичні рекомендації жителям Багдада, як шукати рішення повсякденних проблем? Так само обчислювальній машині немає необхідності пояснювати теорію, яку вона не в змозі зрозуміти. Для машини необхідно тільки, щоб їй поставили відповідні установки, які розрахунки в якому порядку проводити.

Нижче представлений приклад алгоритму, який задається обчислювальній машині. Припустимо, у цієї машини є три осередки пам'яті, в які можна внести відповідні числа. Чи зможете ви порахувати, яким буде результат цього алгоритму?

Етап A. Введіть число 1 в комірку пам'яті № 1, а потім перейдіть до кроку B.

Етап B. Введіть число 1 в комірку пам'яті № 2, а потім перейти до кроку C.

Етап C. Введіть в комірку пам'яті № 3 суму чисел, що знаходяться в осередку пам'яті № 1 і осередку пам'яті № 2, а потім перейдіть до кроку D.

Етап D. Введіть в комірку пам'яті № 1 число з комірки пам'яті № 2, а потім перейдіть до кроку E.

Етап E. Введіть в комірку пам'яті № 2 число з комірки пам'яті № 3, а потім перейдіть до кроку C.

Можна помітити, що машина буде зациклена, так як на етапі Е вона повертається до етапу C. Таким чином, етапи C, D, E будуть повторюватися нескінченно.

Ну що? Ви зрозуміли, що таким чином розраховує машина? Потрібно зовсім небагато часу для того щоб розшифрувати отриману послідовність чисел. Ви можете здогадатися, що цей алгоритм описує послідовність чисел, які нам вже добре відомі, а саме числа Фібоначчі! [21] На етапах А та В були введені перші два члена послідовності: 1 і 1. На етапі C обчислюється сума двох попередніх чисел. На етапах D і Е в пам'ять заносяться наступні числа з ряду таким чином, щоб алгоритм міг працювати циклічно. Якщо ви заходите перевірити, як працює даний алгоритм, то зможете переконатися, що вийде наступна послідовність чисел: 1, 1, 2, 3, 5, 8, 13, 21 і т. Д.

Незважаючи на те, що алгоритм виглядає досить просто на перший погляд, машина Тьюринга все ще не здатна його обробити. Відповідно до визначення, даного їх автором, ця машина не може здійснювати операцію складання, як це зазначено на етапі C. В її функції входять тільки внесення, прочитання і заміна елементів в пам'яті відповідно до інструкцій на кожному етапі. Таким чином, можна задати їй алгоритм складання, згідно з яким числа складаються відповідно до їх розрядами і запам'ятовуванням чисел в розумі, за аналогією з рахунками. Іншими словами, складання не є частиною аксіоматики машини, а це вже одна з її теорем, які повинні мати свій алгоритм для використання. Після того як цей алгоритм буде складено, він може бути використаний на етапі C, і машина Тьюринга, таким чином, вирахує числа Фібоначчі.

Підвищуючи складність завдань, можна навчити машину Тьюринга виконувати операції множення, ділення, піднесення до квадрату, обчислити квадратний корінь, знаходити решеніячно малі величини. Таким чином, за умови складання відповідних алгоритмів машина Тьюринга здатна вирішувати будь-які математичні завдання, які ми вже встигли розглянути, причому точність таких розрахунків буде значно вище.